Quantile-Quantile Plot with Regression Line

A Quantile-Quantile (QQ) Plot with Regression Line is a statistical graphical method for comparing the quantiles of an empirical dataset against those of a theoretical probability distribution. The inclusion of a regression line facilitates the assessment of linearity, providing an additional measure of the goodness-of-fit for the selected distribution.

Method Overview

The .qq_plot_regression() method generates a QQ Plot enhanced by a regression line, allowing for a more detailed visual evaluation of how well the theoretical distribution models the given dataset.

Mathematical Formulation

In a QQ plot, empirical quantiles $Q_{empirical}$ are plotted against theoretical quantiles $Q_{theoretical}$ :

Q_{theoretical} (p) = F^{- 1} (p)

Q_{empirical} (p) = X_{i}

where:

$F^{- 1} (p)$ is the inverse cumulative distribution function (quantile function) of the theoretical distribution.
$X_{i}$ is the $i$ -th order statistic of the sample.
$p_{i}$ is defined as:

p_{i} = \frac{i - 0.5}{n}

where $n$ is the number of observations.

Regression Line

To assess the linear relationship between empirical and theoretical quantiles, a simple linear regression is applied:

Q_{empirical} = β_{0} + β_{1} Q_{theoretical} + ε

where:

$β_{0}$ (intercept) and $β_{1}$ (slope) are estimated using least squares regression.
$ε$ represents the residual error.

If the dataset follows the theoretical distribution, the regression line should have a slope $β_{1}$ close to 1 and an intercept $β_{0}$ close to 0.

Interpretation of Deviations

Points closely following the regression line: The empirical data follows the theoretical distribution.
Deviations from linearity: Indicate skewness, heavy/light tails, or mismatches in distributional assumptions.
Steeper or flatter slopes $β_{1} \neq 1$ : Suggest different variability between empirical and theoretical distributions.

Parameters

General Parameters

id_distribution (str):
Identifier of the theoretical probability distribution under evaluation. The list of supported distributions is available in the Distributions Documentation.
plot_title (str, optional):
The title of the generated plot. (Default: "QQ Plot - Regression")
plot_xaxis_title (str, optional):
The label for the horizontal axis. (Default: "Theoretical Quantiles")
plot_yaxis_title (str, optional):
The label for the vertical axis. (Default: "Sample Quantiles")
plot_legend_title (str | None, optional):
The title for the legend. If set to None, the legend title is omitted. (Default: "Distributions")
plot_height (int, optional):
The height of the plot in pixels. (Default: 400)
plot_width (int, optional):
The width of the plot in pixels. (Default: 600)

QQ Markers Configuration

qq_marker_name (str, optional):
The label assigned to the quantile markers displayed in the legend. (Default: "Markers QQ")
qq_marker_color (str, optional):
The color of the quantile markers, specified in RGBA format. (Default: "rgba(128,128,128,1)")

Regression Line Configuration

regression_line_name (str, optional):
The label assigned to the regression line in the legend. (Default: "Regression")
regression_line_color (str, optional):
The color of the regression line, defined in RGBA format. (Default: "rgba(255,0,0,1)")
regression_line_width (int, optional):
The thickness of the regression line. (Default: 2)

Rendering Options

plotly_plot_renderer ("png" | "jpeg" | "svg" | None, optional):
The format used for exporting the plot when utilizing the Plotly visualization library. If None, the default rendering engine is employed.
plot_engine ("plotly" | "matplotlib", optional):
Specifies the backend library for generating the plot. (Default: "plotly")

Default Usage

The following example illustrates the basic usage of the .qq_plot_regression() method with default parameters:

python

phi.qq_plot_regression(id_distribution="weibull")

This command generates a QQ Plot with Regression Line for the Weibull distribution. The default visualization settings are applied.

Complete Usage

For greater customization, the following example demonstrates how to configure additional parameters:

python

phi.qq_plot_regression(
    id_distribution="normal",
    plot_title="QQ Plot for Normal Distribution",
    plot_xaxis_title="Expected Quantiles",
    plot_yaxis_title="Observed Quantiles",
    plot_legend_title="Comparison",
    plot_height=500,
    plot_width=800,
    qq_marker_name="Empirical Data",
    qq_marker_color="rgba(0,0,255,0.8)",
    regression_line_name="Fitted Line",
    regression_line_color="rgba(255,0,0,1)",
    regression_line_width=3,
    plotly_plot_renderer="svg",
    plot_engine="matplotlib"
)

This implementation allows full control over the plot appearance, color schemes, rendering options, and the choice of plotting library.

Example Visualization

Below is an example visualization of a QQ plot with a regression line:

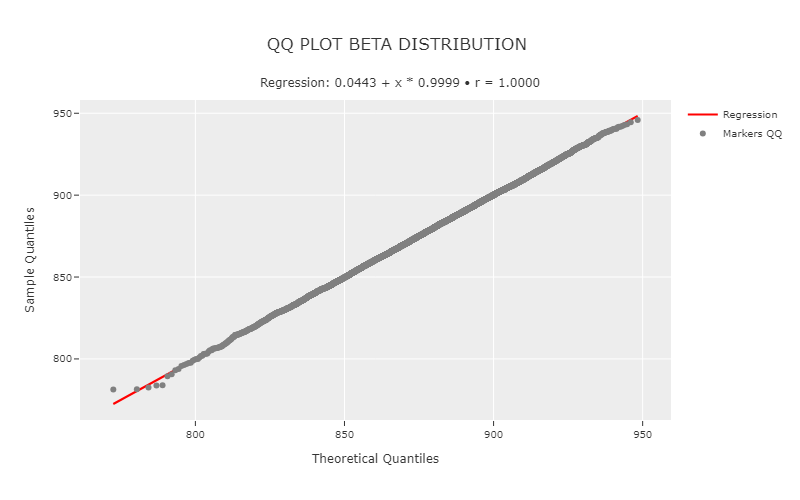
Interpretation

The alignment of points along the regression line indicates that the empirical data closely follows the theoretical distribution, suggesting a good model fit. Deviations from the regression line, however, signal potential mismatches:

Upward curvature: The empirical data has heavier tails than the theoretical distribution.
Downward curvature: The empirical data has lighter tails than the theoretical distribution.
A steeper slope $β_{1} > 1$ : The empirical distribution has greater variability than the theoretical model.
A flatter slope $β_{1} < 1$ : The empirical distribution has lower variability than expected.

If the intercept (\beta_0) is significantly different from zero, it may indicate a shift between the empirical and theoretical distributions.

Quantile-Quantile Plot with Regression Line ​

Method Overview ​

Mathematical Formulation ​

Regression Line ​

Interpretation of Deviations ​

Parameters ​

General Parameters ​

QQ Markers Configuration ​

Regression Line Configuration ​

Rendering Options ​

Default Usage ​

Complete Usage ​

Example Visualization ​

Interpretation ​