Quantile-Quantile Plot

A Quantile-Quantile (QQ) plot is a statistical graphical tool used to compare the quantiles of an empirical dataset against the quantiles of a theoretical probability distribution. This visualization helps assess the goodness-of-fit of the assumed distribution.

Methodology

The QQ plot is constructed using the following steps:

1. Compute the empirical quantiles from the dataset.
2. Compute the theoretical quantiles from the specified distribution.
3. Plot the empirical quantiles on the $y$-axis against the theoretical quantiles on the $x$-axis.

The fundamental equation used to construct the QQ plot is:

$$Q_{\text{theoretical}}(p)=F^{-1}(p)$$$$Q_{\text{empirical}}(p)=X_i$$

where:

• $F^{-1}(p)$ is the quantile function (inverse cumulative distribution function) of the theoretical distribution.
• $X_i$ is the $i$-th order statistic of the empirical data.
• $p$ represents the probability associated with each quantile, typically defined as:

$$p_i=\frac{i-0.5}{n}$$

where $n$ is the total number of observations, and $i$ is the index of the sorted data.

If the empirical data follows the theoretical distribution, the plotted points should align approximately along a 45-degree reference line:

$$y=x$$

Interpretation of Deviations:

• Linear alignment: Indicates a strong fit with the theoretical distribution.
• S-shaped deviations: Suggest discrepancies in the tails, with potentially heavier or lighter tails than the theoretical distribution.
• Curvature (concave or convex): Implies skewness or systematic deviations from the theoretical model.

Applications

The QQ plot is widely used in statistical analysis, including:

• Checking normality assumptions before applying parametric tests.
• Comparing an observed dataset to a theoretical probability distribution.
• Identifying outliers or irregularities in data distributions.

Parameters

The .qq_plot() function generates the QQ plot and accepts the following parameters:

General Parameters

• id_distribution (str):
  Identifier of the theoretical distribution to compare against the empirical dataset. See the list of distributions.

• plot_title (str, optional):
  Title of the QQ plot. Default: "QQ Plot".

• plot_xaxis_title (str, optional):
  Label for the x-axis. Default: "Theoretical Quantiles".

• plot_yaxis_title (str, optional):
  Label for the y-axis. Default: "Sample Quantiles".

• plot_legend_title (str | None, optional):
  Title for the legend. If set to None, no legend title is displayed.

• plot_height (int, optional):
  Height of the plot in pixels. Default: 400.

• plot_width (int, optional):
  Width of the plot in pixels. Default: 600.

Marker Configuration

• qq_marker_name (str, optional):
  Label for the QQ plot markers in the legend. Default: "Markers QQ".

• qq_marker_color (str, optional):
  Marker color in RGBA format. Default: "rgba(128,128,128,1)" (gray).

• qq_marker_size (int, optional):
  Size of the markers. Default: 6.

Rendering Configuration

• plotly_plot_renderer ("png" | "jpeg" | "svg" | None, optional):
  Specifies the format for exporting the plot when using Plotly. If set to None, the default renderer format is applied.

• plot_engine ("plotly" | "matplotlib", optional):
  Specifies the visualization backend. Default: "plotly".

Default Usage

The following example demonstrates the basic usage of the .qq_plot() function with default parameters:

phi.qq_plot(id_distribution="normal")

In this example, the empirical dataset is fitted, and a QQ plot is generated to compare it against a normal distribution.

Complete Usage

A more comprehensive example includes optional parameters to customize the QQ plot’s appearance:

phi.qq_plot(
    id_distribution="weibull",
    plot_title="Weibull QQ Plot",
    plot_xaxis_title="Theoretical Weibull Quantiles",
    plot_yaxis_title="Empirical Quantiles",
    plot_legend_title="QQ Plot Comparison",
    plot_height=500,
    plot_width=700,
    qq_marker_name="Sample Points",
    qq_marker_color="rgba(0,0,255,1)",
    qq_marker_size=8,
    plot_engine="matplotlib"
)

This example customizes the QQ plot’s title, axis labels, marker properties, and rendering engine.

Example Visualization

Below is an example of a QQ plot comparing an empirical dataset to a theoretical distribution.

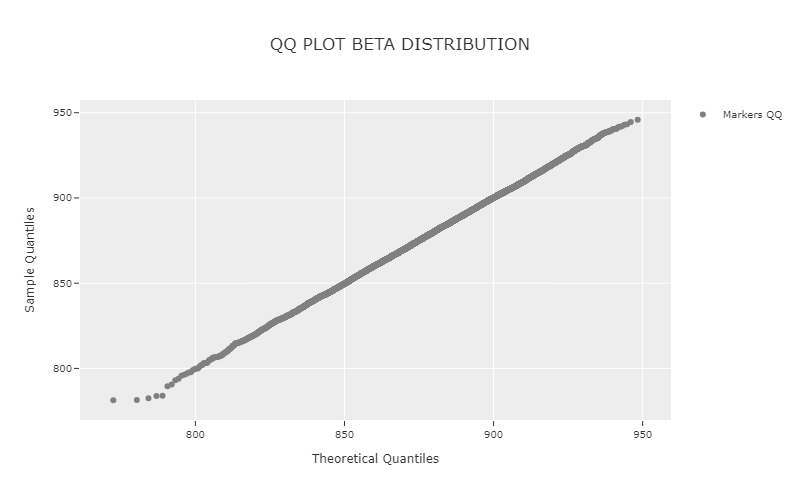
If the empirical data follows the theoretical distribution, the plotted points will align along the 45-degree reference line ($y=x$). Deviations from this line indicate differences between the empirical data distribution and the theoretical model.